Python 拓扑排序
对一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序,是将G中所有顶点排成一个线性序列,使得图中任意一对顶点u和v,若边(u,v)∈E(G),则u在线性序列中出现在v之前。通常,这样的线性序列称为满足拓扑次序(Topological Order)的序列,简称拓扑序列。简单的说,由某个集合上的一个偏序得到该集合上的一个全序,这个操作称之为拓扑排序。
在图论中,由一个有向无环图的顶点组成的序列,当且仅当满足下列条件时,称为该图的一个拓扑排序(英语:Topological sorting):
- 每个顶点出现且只出现一次;
- 若A在序列中排在B的前面,则在图中不存在从B到A的路径。
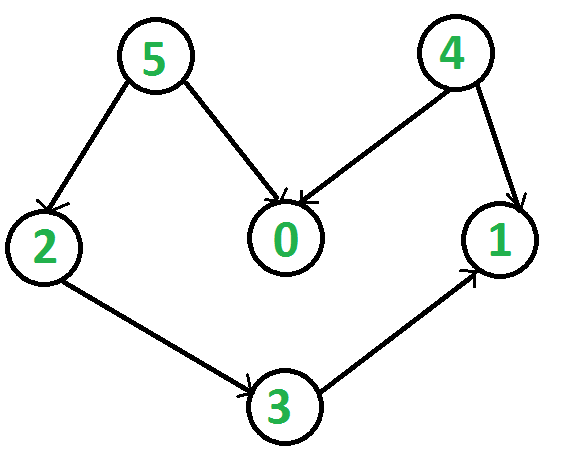
实例
from collections import defaultdict
class Graph:
def __init__(self,vertices):
self.graph = defaultdict(list)
self.V = vertices
def addEdge(self,u,v):
self.graph[u].append(v)
def topologicalSortUtil(self,v,visited,stack):
visited[v] = True
for i in self.graph[v]:
if visited[i] == False:
self.topologicalSortUtil(i,visited,stack)
stack.insert(0,v)
def topologicalSort(self):
visited = [False]*self.V
stack =[]
for i in range(self.V):
if visited[i] == False:
self.topologicalSortUtil(i,visited,stack)
print (stack)
g= Graph(6)
g.addEdge(5, 2);
g.addEdge(5, 0);
g.addEdge(4, 0);
g.addEdge(4, 1);
g.addEdge(2, 3);
g.addEdge(3, 1);
print ("拓扑排序结果:")
g.topologicalSort()
执行以上代码输出结果为:
拓扑排序结果: [5, 4, 2, 3, 1, 0]

 Python3 实例
Python3 实例
smallpang
cws***lpang@126.com
from collections import defaultdict ####发现上面的代码有点问题(不知道是不是我的问题),所以我自己写了一个,同时也加深下对于拓扑的了解 class Graph: # 构造函数 def __init__(self,vertices): # 创建用处存储图中点之间关系的dict{v: [u, i]}(v,u,i都是点,表示边<v, u>, <v, i>):边集合 self.graph = defaultdict(list) # 存储图中点的个数 self.V = vertices # 添加边 def add_edge(self,u,v): # 添加边<u, v> self.graph[u].append(v) # 获取一个存储图中所有点的状态:dict{key: Boolean} # 初始时全为False def set_keys_station(self): keyStation = {} key = list(self.graph.keys()) # 因为有些点,没有出边,所以在key中找不到,需要对图遍历找出没有出边的点 if len(key) < self.V: for i in key: for j in self.graph[i]: if j not in key: key.append(j) for ele in key: keyStation[ele] = False return keyStation # 拓扑排序 def topological_sort(self): # 拓扑序列 queue = [] # 点状态字典 station = self.set_keys_station() # 由于最坏情况下每一次循环都只能排序一个点,所以需要循环点的个数次 for i in range(self.V): # 循环点状态字典,elem:点 for elem in station: # 这里如果是已经排序好的点就不进行排序操作了 if not station[elem]: self.topological_sort_util(elem, queue, station) return queue # 对于点进行排序 def topological_sort_util(self, elem, queue, station): # 设置点的状态为True,表示已经排序完成 station[elem] = True # 循环查看该点是否有入边,如果存在入边,修改状态为False # 状态为True的点,相当于排序完成,其的边集合不需要扫描 for i in station: if elem in self.graph[i] and not station[i]: station[elem] = False # 如果没有入边,排序成功,添加到拓扑序列中 if station[elem]: queue.append(elem) g= Graph(6) g.add_edge(5, 2); g.add_edge(5, 0); g.add_edge(4, 0); g.add_edge(4, 1); g.add_edge(2, 3); g.add_edge(3, 1); print ("拓扑排序结果:") print(g.topological_sort())smallpang
cws***lpang@126.com